Como usar a Matemática no futebol...

Como usar a Matemática no futebol...

Como captar o movimento de uma bola de futebol chutada pelo goleiro?

O goleiro coloca a bola em jogo com um chute forte. A bola sobe até um ponto máximo e começa a descer descrevendo, assim, uma curva que recebeu o nome de parábola. O físico italiano Galileu Galilei, 1564 a 1642, estudou atentamente movimentos como o desta bola e concluiu que, se não fosse a resistência do ar, qualquer corpo solto no campo de gravidade da Terra se movimentaria do mesmo modo. Ou seja, ao fim de 1 segundo percorreria cerca de 5 X 12 = 5 metros;depois de 2 segundos, percorreria cerca de 5 X 22 = 20
metros; depois de 3 segundos, 5 X 32 = 45 metros; e assim sucessivamente. Desta forma, depois de x segundos, percorreria 5 X x2 metros, onde 5 é aproximadamente a metade da aceleração da gravidade em metros por segundo, em cada segundo. Isto é o mesmo que escrever a função f (x) = 5x2. Galileu agrupou todos esses elementos em um importante conceito matemático: função quadrática. Toda função na qual a variável x aparece com o expoente máximo igual a 2 é chamada de função quadrática, ou polinomial de segundo grau, pois o expoente máximo da variável é o quadrado.

função composta

A função composta pode ser entendida pela determinação de uma terceira função C, formada pela junção das funções A e B. Matematicamente falando, temos que f: A → B eg: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.

Exemplo 1
Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:

a) g o f

(g o f)(x) = g(f(x))

g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5

(g o f)(x) = g(f(x)) = 16x² + 5



b) f o g

(f o g)(x) = f(g(x))

f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20

(f o g)(x) = f(g(x)) = 4x² + 20


Exemplo 2
Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.


(g o f)(x) = g(f(x))

g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15

(g o f)(x) = g(f(x)) = 4x² + 16x + 15



(f o g)(x) = f(g(x))

f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1

(f o g)(x) = f(g(x)) = 4x² + 1

os buracos negros não são negros !

Os buracos negros na verdade estão mais para “escurinhos” do que para totalmente negros, mesmo por que de tempos em tempos eles liberam luz. Então se eles liberam luz, eles perdem energia e se não houver mais massa e luz para eles sugarem a sua volta, algum dia eles morrem.

FUNÇÃO AFIM

Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é:

O gráfico de uma função afim é uma reta não perpendicular ao eixo Ox.

Domínio: D = R
Imagem: Im = R São casos particulares de função afim as funções lineares e constante.

Função linear

Uma função definida por f: R→R chama-se linear quando existe uma constante a ∈ R tal que f(x) = ax para todo x ∈ R. A lei que define uma função linear é a seguinte:

O gráfico da função linear é uma reta, não perpendicular ao eixo Ox e que cruza a origem do plano cartesiano.

Domínio: D = R
Imagem: Im = R

Função constante

Uma função definida por f: R→R chama-se constante quando existe uma constante b R tal que f(x) = b para todo x ∈ R. A lei que define uma função constante é:

O gráfico de uma função constante, é uma reta paralela ou coincidente ao eixo Ox q que cruza o eixo Oy no ponto de ordenada b.

Ads by PlusHD.6Ad Options

Coeficientes numéricos

Cada coeficiente numérico de uma função caracteriza um elemento do gráfico dessa função.

• Coeficiente a: coeficiente angular de uma reta. A é igual à tangente do ângulo que a reta faz com o eixo x.

Quando a > 0, a função é crescente.
Quando a < 0, a função é decrescente.

• Coeficiente b: é a ordenada do ponto em que o gráfico de f cruza o eixo das ordenadas, ou seja, b = f(0).

Ads by PlusHD.6Ad Options

Newton's laws

EXERCICIO

EXERCICIO

EXERCICIO

Função Quadrática

Donald no pais da matemagica

POESIA DA MATEMATICA

Aula De Matemática

Pra que dividir sem raciocinar 
Na vida é sempre bom multiplicar 
E por A mais B 
Eu quero demonstrar 
Que gosto imensamente de você 

Por uma fração infinitesimal, 
Você criou um caso de cálculo integral 
E para resolver este problema 
Eu tenho um teorema banal 

Quando dois meios se encontram desaparece a fração 
E se achamos a unidade 
Está resolvida a questão 

Pra finalizar, vamos recordar 
Que menos por menos dá mais amor 
Se vão as paralelas 
Ao infinito se encontrar 
Por que demoram tanto os corações a se integrar? 
Se infinitamente, incomensuravelmente, 
Eu estou perdidamente apaixonado por você

Poesia Matemática

Às folhas tantas
do livro matemático
um Quociente apaixonou-se
um dia
doidamente
por uma Incógnita.
Olhou-a com seu olhar inumerável
e viu-a do ápice à base
uma figura ímpar;
olhos rombóides, boca trapezóide,
corpo retangular, seios esferóides.
Fez de sua uma vida
paralela à dela
até que se encontraram
no infinito.
"Quem és tu?", indagou ele
em ânsia radical.
"Sou a soma do quadrado dos catetos.
Mas pode me chamar de Hipotenusa."
E de falarem descobriram que eram
(o que em aritmética corresponde
a almas irmãs)
primos entre si.
E assim se amaram
ao quadrado da velocidade da luz
numa sexta potenciação
traçando
ao sabor do momento
e da paixão
retas, curvas, círculos e linhas sinoidais
nos jardins da quarta dimensão.
Escandalizaram os ortodoxos das fórmulas euclidiana
e os exegetas do Universo Finito.
Romperam convenções newtonianas e pitagóricas.
E enfim resolveram se casar
constituir um lar,
mais que um lar,
um perpendicular.
Convidaram para padrinhos
o Poliedro e a Bissetriz.
E fizeram planos, equações e diagramas para o futuro
sonhando com uma felicidade
integral e diferencial.
E se casaram e tiveram uma secante e três cones
muito engraçadinhos.
E foram felizes
até aquele dia
em que tudo vira afinal
monotonia.
Foi então que surgiu
O Máximo Divisor Comum
freqüentador de círculos concêntricos,
viciosos.
Ofereceu-lhe, a ela,
uma grandeza absoluta
e reduziu-a a um denominador comum.
Ele, Quociente, percebeu
que com ela não formava mais um todo,
uma unidade.
Era o triângulo,
tanto chamado amoroso.
Desse problema ela era uma fração,
a mais ordinária.
Mas foi então que Einstein descobriu a Relatividade
e tudo que era espúrio passou a ser
moralidade
como aliás em qualquer
sociedade

Millôr Fernandes

Video função quadrática

função quadratica

função quadrática

função quadrática

Função Composta

 

A função composta pode ser entendida pela determinação de uma terceira função C, formada pela junção das funções A e B. Matematicamente falando, temos que f: A → B e g: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.

Exemplo 1

Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:

a) g o f

(g o f)(x) = g(f(x))

g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5

(g o f)(x) = g(f(x)) = 16x² + 5



b) f o g

(f o g)(x) = f(g(x))

f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20

(f o g)(x) = f(g(x)) = 4x² + 20


Exemplo 2

Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.


(g o f)(x) = g(f(x))

g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15

(g o f)(x) = g(f(x)) = 4x² + 16x + 15



(f o g)(x) = f(g(x))

f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1

(f o g)(x) = f(g(x)) = 4x² + 1



Por Marcos Noé
Graduado em Matemática

Professor de matemática dá dicas para a prova do Enem na Uerj

Universidade é um dos principais pontos de prova no Rio.
Alunos aprovam iniciativa e aproveitam as dicas de última hora.

Professor de matemática Márcio Barbosa dá aulas em frente ao portão principal da Uerj (Foto: Mariucha Machado / G1)

A poucas horas do início do Exame Nacional do Ensino Médio (Enem), previsto para as 13h deste sábado (26), o professor de matemática Márcio Barbosa dava as últimas dicas para os alunos que chegavam à Universidade Estadual do Rio de Janeiro (Uerj), nesta manhã. O local é um dos principais pontos de prova do Rio.

Enquanto os alunos vão chegando, o professor dá dicas de como resolver de forma rápida e simples algumas questões. "Eu estou relaxando as pessoas fazendo cálculos e resolvendo problemas. Enquanto eles acompanham, acabam esquecendo as preocupações", afirmou Barbosa, que desenvolve o projeto em vias públicas do Centro do Rio.

Depois que dá as explicações, o professor oferece DVDs com aulas que dão dicas de matemática. Cada DVD é vendido por R$20.

O estudante Rosiel Lima, de 25 anos, aprovou a aula do professor e vai tentar fazer curso de engenharia civil na Uerj ou UFRJ. "Ele consegue resolver em segundos o que a gente precisa de minutos".

Sobre o exame
A edição de 2013 do Enem tem 7.173.574 candidatos inscritos. As provas acontecem neste sábado e domingo (27) em 1.661 municípios. Os gabaritos das provas objetivas serão divulgados na página do Inep até o dia 30 de outubro de 2013. A data do resultado individual ainda não foi divulgada.

O G1 traz a cobertura completa do Enem 2013 em todo o Brasil. Nas noites de sábado e domingo, após as provas, o G1 terá um programa ao vivo ouvindo os comentários dos professores do Projeto Educação, da Globo Nordeste, e do cursinho De A a Z, do e do Rio de Janeiro. Também vai publicar a resolução das questões do Enem feitas por professores dos cursos pré-vestibulares Etapa, Oficina do Estudante e Objetivo.

Referencias : http://g1.globo.com/educacao/enem/2013/noticia/2013/10/professor-de-matematica-da-dicas-para-prova-do-enem-na-uerj.html

Postado Por : Thaywan Talles

Jogo Multiplicativo

Jogo Multiplicativo

Organização da turma

• Grupos com quatro alunos ou mais cada. Como variação o professor pode conduzir o jogo com a classe toda.

Recursos

• Sete cartas onde estão marcados um dos seguintes números: 2, 3, 4, 5, 7, 8 e 9.

Objetivo do jogo

• Trabalhar com os alunos a memorização da tabuada, a capacidade de análise, a formulação de hipóteses e a tomada de decisões na resolução de problemas.

Regras

• O jogo pode ser feito em grupos de qutro ou mais alunos.
• Uma pessoa do grupo escolhe quatro cartas, sem que os demais vejam.
• A tarefa dos outros jogadores é tentar ser o primeiro a adivinhar as quatro cartas.
• Na sua vez de jogar, ao jogador só é permitido fazer a pergunta: você tem duas cartas cujo produto é ____ (15, por exemplo).
• O jogador que tem as cartas na mão responde sim ou não.
• Os produtos são registrados em um papel para que todos possam analisar as tentativas, bem como as respostas "sim" ou "não".
• O vencedor é aquele que conseguir dizer, em primeiro lugar, quais são todas as quatro cartas escolhidas.
• Se a resposta não estiver correta, o jogador perde a vez de jogar.

Professor
Baixe as regras do jogo para impressão .http://www.matematica.seed.pr.gov.br/arquivos/File/jogo_multiplicativo_regras.pdf

Função afim

Função afim

A função afim, também conhecida como função de 1º grau, obedece a seguinte lei:

y = ax + b

onde a e b são números reais e a0.

 Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.

 Veja alguns exemplos de funções polinomiais do 1º grau:

 f(x) = 5x - 3, onde a = 5 e b = - 3
 f(x) = -2x - 7, onde a = -2 e b = - 7
 f(x) = 11x, onde a = 11 e b = 0

onde podem ocorrer nos seguintes casos: onde a > 0 ou a < 0, observe abaixo:

1º caso: a > 0 teremos então uma função crescente, pois a medida que o valor atribuido a x aumenta, os valores pra y também aumentam. 

ex: f(x) = x + 2

 

Atribuimos valores a x : basta substituir o valor atribuido no lugar de x.

para x = -2 , teremos y = -2+2 = 0 (-2,0)

para x = -1 , teremos y = -1+2 = 0 (-1,1)

para x = 0 , teremos y = 0+2 = 0 (0,2)

para x = 1 , teremos y = 1+2 = 0 (1,3)

para x = 2 , teremos y = 2+2 = 0 (2,4)

Logo o Dom = |R e Img (f) = |R.

2º caso: a < 0 teremos então uma função decrescente, pois a medida que aumentam os valores de x, diminuem os valores de y.

ex: y = -x + 2

O mesmo processo que fazemos na crescente, fazemos na decrescente. Atribuimos valores a x, para acharmos y, e assim formarmos o par ordenado.

Os pares ordenados são os seguintes : para x = -2 =>(-2,4)

                                                           para x = -1 => (-1,3)

                                                           para x = 0 => (0,2)

                                                           para x = 1 => (1,1)

                                                           para x = 2 => (2,0)

onde o Dom = |R e a Img (f) = |R. 

Para encontramos a raiz da função, igualamos f(x) = 0 => ax + b = 0 => x = -b dividido por a.

ex: y = x + 2 , a raiz dessa função é -2/1 = -2

     y = -x + 2, a raiza dessa função é - 2/ -1 = 2/1 = 2. 

Observe os graficos acima, veja qual é o ponto em que a reta corta em x, são exatamnete as raizes encontradas, logo concluimos que as raizes são os pontos em que a reta corta em x.

Estudo dos sinais: Estudar o sinal de uma qualquer y = f(x) é determinar os valor de x para os quais y é positivo, os valores de x para os quais y é zero e os valores de x para os quais y é negativo. Então vamos lá.. pra quem gosta de um bom macetinha ai vai a dica!

 macetinho para estudo de sinais 

 ex: y = 2x - 4

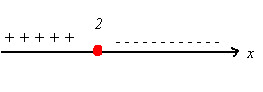
 tomamos a raiz como "centro" (ponto de partida) vemos qual é o sinal de a, neste caso a é positivo, então vamos ao macetinho: " a direita da raiz é o sinal de a, e a esquerda da raiz sinal contrario de a", obeserve que -b/a = 2 (que é nossa raiz) 

 

Se fosse y = -2x - 4, teriamos a raiz igual a 2 também, mais o estudo de sinais mudaria, porque o nosso a é negativo, obeserve.

Mais porque mudou ? simples u.u

Lembra do macetinho? então.. nesse caso o a é negativo, então o sinal que vai ficar a direita da raiz também é negativo!

Postado por: Thaywan Talles

Letra do funk da função quadratica

Se liga ai galera no que eu vou falar,

essa canção vocês vão ter que estudar,

pro vestibular ela é fundamental,

é a famosa função do segundo grau.

Seu grafico da função é a parabola,

sua concavidade depende do A... do A... do A,

se é positivo feliz ela está,

mas se está triste é porque negativo é o A,

corta o eixo Y no zero C,

e das raizes tem que saber,

que a soma é menos B sobre A,

e o produto C sobre A.

E o X do vertice... da parabola,

vale menos B sobre dois A... é..sobre dois A.

E o Y do V .. eh eh.. da parabola,

vale menos delta sobre quatro A.. sobre quatro A.

 

 

 

 

REFERENCIA: http://tudo-matematica.blogspot.com.br/search?updated-max=2011-09-04T07:50:00-07:00&max-results=7

Exercícios sobre Função de 2º Grau

Teste os seus conhecimentos: Faça exercícios sobre Função de 2º Grau e veja a resolução comentada.

 

1° )  Calcule o valor de k de modo que a função f(x) = 4ax² – 4x – k não tenha raízes, isto é, o gráfico da parábola não possui ponto em comum com o eixo x.

∆ < 0
b² – 4ac < 0
(–4)² – 4 * 4 * (–k) < 0
16 + 16k < 0
16k < – 16
k < –1
O valor de k para que a função não tenha raízes reais deve ser menor que – 1.

2°) Determine os valores de p, para que a função f(x) = (m – 2)x² – 2x + 6 admita raízes reais.

Para essa situação temos que ∆ ≥ 0.

∆ ≥ 0
b² – 4ac ≥ 0
(–2)² – 4 * (m – 2) * 6 ≥ 0
4 – 4 * (6m – 12) ≥ 0
4 – 24m + 48 ≥ 0
– 24m ≥ – 48 – 4
– 24m ≥ – 52
24m ≤ 52
m ≤ 52/24
m ≤ 13/6
O valor de m que satisfaça a condição exigida é m ≤ 13/6.

3°)  (Vunesp-SP) O gráfico da função quadrática definida por y = x² – mx + (m – 1), em que m Є R, tem um único ponto em comum com o eixo das abscissas. Determine y associado ao valor de x = 2.

 Um ponto em comum significa dizer uma única raiz, então ∆ = 0.

y = x² – mx + (m – 1)
Substituir m = 2, no intuito de obter a lei da função
y = x² – 2x + (2 – 1)
y = x² – 2x +1
Substituindo x = 2, para determinarmos o valor de y
y = 2² – 2 * 2 + 1
y = 4 – 4 + 1
y = 1
Temos que a equação possui a lei de formação y = x² – 2x +1. E quando x = 2, o valor de y se torna igual a 1.
 

4°)  (UCSal-BA) Determine os pontos de intersecção da parábola da função f(x) = 2x² – 3x + 1, com o eixo das abscissas.

No instante em que a parábola cruza o eixo das abscissas o valo de y ou f(x) é igual a zero. Portanto:
f(x) = 0
2x² – 3x + 1 = 0



Os pontos de interseção são:
x = 1 e y = 0
x = 1/2 e y = 0

REFERENCIA: http://exercicios.brasilescola.com/matematica/exercicios-sobre-funcao-2-o-grau.htm#questao-2139

 

Funções de Segundo Grau

 

1. O grau de uma função

O grau de uma variável independente é dado pelo seu expoente. Assim, as funções de segundo grau são dadas por um polinômio de segundo grau, e o grau do polinômio é dado pelo monômio de maior grau.

Portanto, as funções de segundo grau têm a variável independente com grau 2, ou seja, o seu maior expoente é 2. O gráfico que corresponde a essas funções é uma curva denominada parábola.

No dia-a-dia, há muitas situações definidas pelas funções de segundo grau. A trajetória de uma bola lançada para a frente é uma parábola. Se fizermos vários furos em várias alturas num bote cheio de água, os pequenos jorros de água que saem pelos furos descrevem parábolas. A antena parabólica tem a forma de parábola, originando o seu nome.

2. Definição

Em geral, uma função quadrática ou polinomial do segundo grau é expressa da seguinte forma:

f (x) = ax2 + bx + c, onde a 0

Observamos que aparece um termo de segundo grau, ax². É essencial que exista um termo de segundo grau na função para que ela seja uma função quadrática, ou de segundo grau. Além disso, esse termo deve ser o de maior grau da função, pois se houvesse um termo de grau 3, isto é, ax³, ou de grau superior, estaríamos falando de uma função polinomial de terceiro grau.  

Assim como os polinômios podem ser completos ou incompletos, temos funções de segundo grau incompletas, como:

f (x) = x2 f (x) = ax2 f (x) = ax2+ bx f (x) = ax2 + c

Pode acontecer de o termo de segundo grau aparecer isoladamente, como na expressão geral y = ax²; acompanhado por um termo de primeiro grau, como no caso geral y = ax² + bx; ou também unido a um termo independente ou a um valor constante, como em y = ax² + c.

É comum pensarmos que a expressão algébrica de uma função quadrática é mais complexa que a das funções lineares. Normalmente, também supomos que sua representação gráfica é mais complicada. Mas não é sempre assim. Além disso, os gráficos das funções quadráticas são curvas muito interessantes, conhecidas como parábolas.

Figura 3

3. Representação gráfica da função y = ax²

Como acontece com toda função, para representá-la graficamente temos, antes, de construir uma tabela de valores (Figura 3, ao lado).

Começamos representando a função quadrática y = x², que é a expressão mais simples da função polinomial de segundo grau.

Se unirmos os pontos com uma linha contínua, o resultado é uma parábola, como mostra a Figura 4, abaixo:

Figura 4

Observando atentamente a tabela de valores e a representação gráfica da função y = x² vamos perceber que o eixo Y, das ordenadas, é o eixo de simetria do gráfico.

Além disso, o ponto mais baixo da curva (aquele em que a curva se intercepta com o eixo Y) é o ponto de coordenadas (0, 0). Este ponto é conhecido como vértice da parábola.

Figura 5

Na Figura 5, ao lado, estão as representações gráficas de várias funções que têm como expressão geral y = ax².

Observando com atenção a Figura 5 podemos afirmar:

• O eixo de simetria de todos os gráficos é o eixo Y.
Como x² = (– x)², a curva é simétrica em relação ao eixo das ordenadas.

• A função y = x² é crescente para x > x_v e decrescente para x < x_v. Trata-se de uma função contínua, pois para pequenas variações de x correspondem pequenas variações de y.

• Todas as curvas têm o vértice no ponto (0,0).

• Todas as curvas que estão no semiplano de ordenadas positivas, com exceção do vértice V (0,0), têm ponto de mínimo que é o próprio vértice.

•  Todas as curvas que estão no semiplano de ordenadas negativas, com exceção do vértice V (0,0), têm ponto de máximo que é o próprio vértice.

• Se o valor de a for positivo, os ramos da parábola se dirigem para cima. Ao contrário, se a for negativo, os ramos se dirigem para baixo. Dessa forma, o sinal do coeficiente determina a orientação da parábola:

a > 0, a parábola abre-se para valores positivos de y. a < 0, a parábola abre-se para valores negativos de y.

•	À medida que aumenta o valor absoluto de a, a parábola é mais fechada, isto é, os ramos ficam mais próximos do eixo de simetria: quanto maior |a|, mais a parábola se fecha.
•	Os gráficos de y = ax2 e y = –ax2 são simétricos entre si com relação ao eixo X, das abscissas.

Figura 6